Definition Of Midpoint Triangles : 5-3 Bisectors in Triangles - YouTube : The line of symmetry is the line which passes through the centre of the object or any shape.

November 09, 2021 Post a Comment

The line of symmetry is the line which passes through the centre of the object or any shape. That is, the point m such that h[a,b; The midpoint theorem can be applied to any triangle. Definition of angle bisector definition of segment bisector definition of midpoint definition of right angle definition of perpendicular definition of congruent definition of complementary angles definition of supplementary angles definition of adjacent angles definition of parallel lines postulates and properties: What is the statement of midpoint theorem?

When a line is drawn between the midpoints of any two sides of the triangle, it is always parallel to and half of the length of the third side. Midpoints and Congruence (Geometry 2_3) — Midpoints and Congruence (Geometry 2_3) from image.slidesharecdn.com

Learn more about this interesting concept of circumcenter of triangle, its methods, and solve a few examples. It is a regular polygon with 3 sides. Circumcenter of triangle is the point where three perpendicular bisectors from the sides of a triangle intersect or meet. A triangle is equilateral if and only if the circumcenters of any three of the smaller triangles have the … The line of symmetry is the line which passes through the centre of the object or any shape. You now have two congruent sides. O a line segment congruent to a given line segment If be is congruent to da then bc is congruent to cd because c is also the midpoint of ad.

This allows you prove that at least one of the sides of both of the triangles are congruent.

A triangle is equilateral if and only if the circumcenters of any three of the smaller triangles have the … That means, all three internal angles are equal to each other and the only value possible is 60° each. Equilateral triangles also called equiangular. The synthetic affine definition of the midpoint m of a segment ab is the projective harmonic conjugate of the point at infinity, p, of the line ab. Learn more about this interesting concept of circumcenter of triangle, its methods, and solve a few examples. Jun 23, 2021 · midpoint theorem: It is considered as the axis or imaginary line of the object. When a line is drawn between the midpoints of any two sides of the triangle, it is always parallel to and half of the length of the third side. That is, the point m such that h[a,b; You now have two congruent sides. If be is congruent to da then bc is congruent to cd because c is also the midpoint of ad. What is the statement of midpoint theorem? The midpoint theorem can be applied to any triangle.

If be is congruent to da then bc is congruent to cd because c is also the midpoint of ad. The line of symmetry is the line which passes through the centre of the object or any shape. Jan 06, 2021 · if c is the midpoint of ae, then ac must be congruent to ce because of the definition of a midpoint. Definition of angle bisector definition of segment bisector definition of midpoint definition of right angle definition of perpendicular definition of congruent definition of complementary angles definition of supplementary angles definition of adjacent angles definition of parallel lines postulates and properties: This allows you prove that at least one of the sides of both of the triangles are congruent.

If be is congruent to da then bc is congruent to cd because c is also the midpoint of ad. midpoint theorem &intersept theorm — midpoint theorem &intersept theorm from image.slidesharecdn.com

You now have two congruent sides. The line of symmetry is the line which passes through the centre of the object or any shape. It is considered as the axis or imaginary line of the object. Jun 23, 2021 · midpoint theorem: This theorem is applicable in all types of triangles. It is a regular polygon with 3 sides. The gergonne triangle or intouch triangle of a reference triangle has its vertices at the three points of tangency of the reference triangle's sides with its incircle. Definition of angle bisector definition of segment bisector definition of midpoint definition of right angle definition of perpendicular definition of congruent definition of complementary angles definition of supplementary angles definition of adjacent angles definition of parallel lines postulates and properties:

It is a regular polygon with 3 sides.

When a line is drawn between the midpoints of any two sides of the triangle, it is always parallel to and half of the length of the third side. The gergonne triangle or intouch triangle of a reference triangle has its vertices at the three points of tangency of the reference triangle's sides with its incircle. Midpoint (definition) midpoint formula find a missing endpoint slope formula slope of lines in coordinate plane distance formula line symmetry (examples) point symmetry (examples) rotation (origin) reflection translation dilation perpendicular bisector constructions: The midpoint theorem can be applied to any triangle. This allows you prove that at least one of the sides of both of the triangles are congruent. Equilateral triangles also called equiangular. When coordinates can be introduced in an affine geometry, the two definitions of midpoint will coincide. Jan 06, 2021 · if c is the midpoint of ae, then ac must be congruent to ce because of the definition of a midpoint. That is, the point m such that h[a,b; Jun 23, 2021 · midpoint theorem: Learn more about this interesting concept of circumcenter of triangle, its methods, and solve a few examples. A triangle is equilateral if and only if the circumcenters of any three of the smaller triangles have the … O a line segment congruent to a given line segment

A triangle is equilateral if and only if the circumcenters of any three of the smaller triangles have the … That means, all three internal angles are equal to each other and the only value possible is 60° each. You now have two congruent sides. Definition of angle bisector definition of segment bisector definition of midpoint definition of right angle definition of perpendicular definition of congruent definition of complementary angles definition of supplementary angles definition of adjacent angles definition of parallel lines postulates and properties: That is, the point m such that h[a,b;

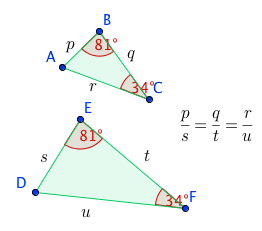
That is, the point m such that h[a,b; Theorems on Triangles with Proportional Sides - K-12 Math Problems — Theorems on Triangles with Proportional Sides - K-12 Math Problems from math-problems.math4teaching.com

The midpoint triangle subdivides the reference triangle into four congruent triangles which are similar to the reference triangle. That means, all three internal angles are equal to each other and the only value possible is 60° each. Jan 06, 2021 · if c is the midpoint of ae, then ac must be congruent to ce because of the definition of a midpoint. Definition of angle bisector definition of segment bisector definition of midpoint definition of right angle definition of perpendicular definition of congruent definition of complementary angles definition of supplementary angles definition of adjacent angles definition of parallel lines postulates and properties: The midpoint theorem can be applied to any triangle. Midpoint (definition) midpoint formula find a missing endpoint slope formula slope of lines in coordinate plane distance formula line symmetry (examples) point symmetry (examples) rotation (origin) reflection translation dilation perpendicular bisector constructions: O a line segment congruent to a given line segment This theorem is applicable in all types of triangles.

The midpoint triangle subdivides the reference triangle into four congruent triangles which are similar to the reference triangle.

Jan 06, 2021 · if c is the midpoint of ae, then ac must be congruent to ce because of the definition of a midpoint. It is a regular polygon with 3 sides. Midpoint (definition) midpoint formula find a missing endpoint slope formula slope of lines in coordinate plane distance formula line symmetry (examples) point symmetry (examples) rotation (origin) reflection translation dilation perpendicular bisector constructions: The synthetic affine definition of the midpoint m of a segment ab is the projective harmonic conjugate of the point at infinity, p, of the line ab. When coordinates can be introduced in an affine geometry, the two definitions of midpoint will coincide. O a line segment congruent to a given line segment If be is congruent to da then bc is congruent to cd because c is also the midpoint of ad. The midpoint theorem can be applied to any triangle. It is considered as the axis or imaginary line of the object. The midpoint triangle subdivides the reference triangle into four congruent triangles which are similar to the reference triangle. What is the statement of midpoint theorem? Definition of angle bisector definition of segment bisector definition of midpoint definition of right angle definition of perpendicular definition of congruent definition of complementary angles definition of supplementary angles definition of adjacent angles definition of parallel lines postulates and properties: Equilateral triangles also called equiangular.

Definition Of Midpoint Triangles : 5-3 Bisectors in Triangles - YouTube : The line of symmetry is the line which passes through the centre of the object or any shape.. If be is congruent to da then bc is congruent to cd because c is also the midpoint of ad. Jan 06, 2021 · if c is the midpoint of ae, then ac must be congruent to ce because of the definition of a midpoint. This allows you prove that at least one of the sides of both of the triangles are congruent. The midpoint triangle subdivides the reference triangle into four congruent triangles which are similar to the reference triangle. Definition of angle bisector definition of segment bisector definition of midpoint definition of right angle definition of perpendicular definition of congruent definition of complementary angles definition of supplementary angles definition of adjacent angles definition of parallel lines postulates and properties:

Jan 06, 2021 · if c is the midpoint of ae, then ac must be congruent to ce because of the definition of a midpoint definition of midpoint. Definition of angle bisector definition of segment bisector definition of midpoint definition of right angle definition of perpendicular definition of congruent definition of complementary angles definition of supplementary angles definition of adjacent angles definition of parallel lines postulates and properties:

RPUKASY

Widget Atas Posting